PROJECT #0 – C++ PRIMER

发布于 2022-08-30  842 次阅读

Overview

本学期所有的编程项目都将在BusTub数据库管理系统上编写。这个系统是用C++编写的。为了确保你有必要的C++背景，我们要求每个人完成一个简单的编程任务，以评估你对C++基本功能的了解。这个项目不会给你打分，但你必须以满分完成这个项目，才允许继续学习。任何学生如果不能在截止日期前完成这项作业，将被要求退出该课程。

这个编程作业中的所有代码都必须用C++（特别是C++17）编写。如果你以前没有使用过C++，这里有一个关于该语言的简短教程，一般来说知道C++11就足够了。在cppreference上有更多关于语言内部的详细文档。A Tour of C++和Effective Modern C++也可以从CMU图书馆以数字形式获得。

PROJECT SPECIFICATION

在这个项目中，你将实现三个类。矩阵、RowMatrix和RowMatrixOperations。这些矩阵是简单的二维矩阵，必须支持加法、矩阵乘法和一个简化的通用矩阵乘法（GEMM）操作。

你只需要修改一个文件：p0_starter.h 你可以在BusTub资源库中找到这个文件，地址是 src/include/primer/p0_starter.h。

在这个头文件中，我们定义了你必须实现的三个类。Matrix抽象类定义了派生类RowMatrix的公共函数。RowMatrixOperations类使用RowMatrix对象来实现上面概述中提到的操作。文件中指定了函数原型和成员变量。该项目要求你填写所有构造函数、解构函数和成员函数的实现。不要添加任何额外的函数原型或成员变量。你的实现应该只包括实现我们为你定义的函数。

教员和助教不会对C++问题提供任何帮助。你可以自由使用谷歌或StackOverflow来了解C++和你遇到的任何错误。

TESTING

你可以使用我们的测试框架来测试这项任务的各个组成部分。我们使用GTest进行单元测试案例。有一个文件包含对所有三个类的测试。

启动器：test/primer/starter_test.cpp
你可以在命令行中单独编译和运行每个测试。

$ mkdir build
$ cd build
$ make starter_test
$ ./test/starter_test

你也可以运行 make check-tests 来运行所有的测试案例。注意，有些测试是禁用的，因为你还没有实施未来的项目。你可以在GTest中通过给测试名称添加DISABLED_前缀来禁用测试。

这些测试只是所有测试的一个子集，我们将用它来评估和评定你的项目。你应该自己编写额外的测试用例来检查你的实现的完整功能。

请确保你从测试名称中删除DISABLED_前缀，否则它们将无法运行。

配置环境

首先是创建环境，这里我直接借用朋友的服务器，上面已经有配置好的Linux环境以及cpp的各种工具比如cmake、gdb、gcc等

这里我采用的是2021的版本，直接在服务器对应的位置

git clone https://github.com/cmu-db/bustub.git 克隆到自己的服务器上

这里有一个小坑，就是clone下来会报头文件路径找不到的错误，这里就需要我们配置c_cpp_properties.json了

1) 点击 Ctrl + Shift +P  弹出命令搜索框；2) 选择  C/C++: 编辑配置 (UI)  即可生成 c_cpp_properties.json 文件，此文件同样包含在.vscode文件夹中。

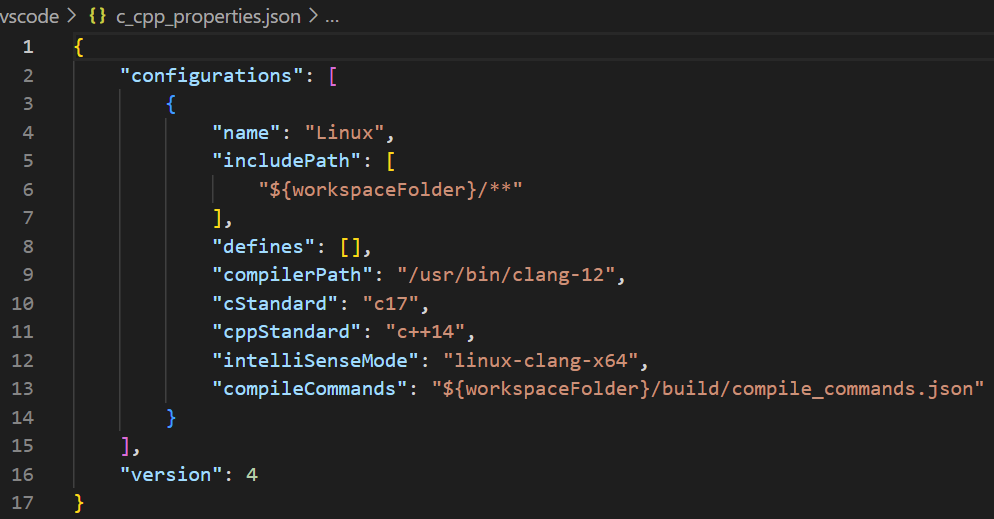
注意这里一定要在最外层的文件夹下进行配置，这样所有cpp的头文件路径就都不会报错了
在上述配置文件中，我们会看到类似于  ${workspaceFolder}  等等类似的描述，这些描述是 VS Code 预定义变量名，可以用来代指工作目录的路径，环境变量的名称，生成文件的名称等等。使用这些预定义的变量名可以使得我们的开发过程更加高效，同时可移植性也大大增强。

⭐一般我们比较常见的变量名有：

${workspaceFolder} - VS Code当前打开工作区文件夹的路径
${file} - 当前打开文件的绝对路径
${fileBasename} - 当前打开文件的名称
${fileBasenameNoExtension} - 当前打开文件的名称，但是不加后缀名
${fileDirname} - 文件所在的文件夹路径

代码内容


主要实现三个类：matrix，RowMatrix，RowMatrixOperations

matrix


是个抽象类，定义了矩阵这个类所需要的一些基本成员变量和函数：

因为大部分是虚函数，所以不需要我们填写实现

需要做的是在构造函数里初始化一些变量：rows，columns，以及初始化一个一维数组，用来保存flatten matrix的内容，注意因为动态申请的内存，里面的内容并不确定，所以最好在

构造函数里将其初始化为0

此外，需要在析构函数里释放掉数组

Matrix(int rows, int cols) {
    rows_ = rows;
    cols_ = cols;
    int len = rows * cols;
    linear_ = new T[len];
  }

注意，这里的linear_是指向二维数组那个空间的头指针，直接从这个头指针申请rows*cols个大小的堆空间即可

RowMatrix


继承Matrix类，并实现成员函数：

基本上都很直观，另外这里增加了成员变量，二级指针data,因此我们在构造函数里需要根据rows和cols来申请一个二维数组，注意需要先申请一个一维指针数组，然后每个元素存放一个指向一维数组的指针。在析构函数中，同样需要首先delete掉每个元素对应的数组，然后delete掉这个指针数组

RowMatrix(int rows, int cols) : Matrix<T>(rows, cols) {
    data_ = new T *[rows];
    for (int i = 0; i < rows; i++) {
      data_[i] = this->linear_ + i * cols;
    }
  }
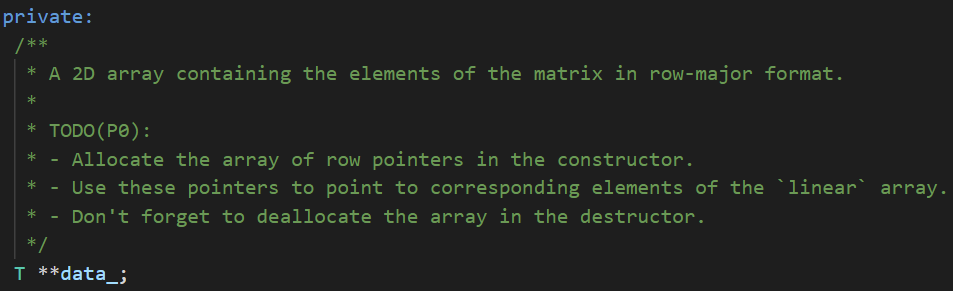
在构造函数中分配行指针数组，使用这些指针指向“线性”数组的相应元素，不要忘记在析构函数中释放数组。

data_即二维数组对应的指针，首先data_ = new T *[rows];表示data_申请了rows个大小的指针数组

然后data_[i] = this->linear_ + i * cols;表示把这个指针数组中的每个空间对应的指针都指向我们之前已经申请好的内存空间，this->linear就是初始地址，第一行指针指向this->linear_ + 0 * cols，第二行指针指向this->linear_ + 1 * cols然后依次类推

这样整理好之后，对应的data_[i][j]就是我们想要的二维数组了，即matrix对应的形式

RowMatrixOperations

这里需要实现几个矩阵运算的函数：加法和乘法，也很简单

复杂的点在于，函数的参数类型是unique_ptr,智能指针

unique_ptr

代表这个指针指向的资源只属于一个owner，因此不能赋值给其他变量，注意，直接作为函数参数，也是一种赋值

即，他不能copy，只能move

Add函数，即两个矩阵相加，对应每个元素相加即可

static auto Add(const RowMatrix<T> *matrixA, const RowMatrix<T> *matrixB) -> std::unique_ptr<RowMatrix<T>> {
    // TODO(P0): Add implementation
    if (matrixA->GetRowCount() != matrixB->GetRowCount() || matrixA->GetColumnCount() != matrixB->GetColumnCount())
      return std::unique_ptr<RowMatrix<T>>(nullptr);

    int row = matrixA->GetRowCount();
    int col = matrixA->GetColumnCount();
    auto addMatrix = std::unique_ptr<RowMatrix<T>>(new RowMatrix<T>(row, col));
    for (int i = 0; i < row; i++) {
      for (int j = 0; j < col; j++) {
        T sum = matrixA->GetElement(i, j) + matrixB->GetElement(i, j);
        addMatrix->SetElement(i, j, sum);
      }
    }
    return addMatrix;
  }

Multiply函数，即两个矩阵相乘

static auto Multiply(const RowMatrix<T> *matrixA, const RowMatrix<T> *matrixB) -> std::unique_ptr<RowMatrix<T>> {
    // TODO(P0): Add implementation

    int rowA = matrixA->GetRowCount();
    int colA = matrixA->GetColumnCount();
    int rowB = matrixB->GetRowCount();
    int colB = matrixB->GetColumnCount();
    if (colA != rowB) return std::unique_ptr<RowMatrix<T>>(nullptr);

    auto multMatrix = std::unique_ptr<RowMatrix<T>>(new RowMatrix<T>(rowA, colB));
    int common = colA;
    for (int i = 0; i < rowA; i++) {
      for (int j = 0; j < colB; j++) {
        T sum = 0;
        for (int k = 0; k < common; k++) {
          sum += matrixA->GetElement(i, k) * matrixB->GetElement(k, j);
        }
        multMatrix->SetElement(i, j, sum);
      }
    }
    return multMatrix;
  }

这里需要注意的就是我们用到了unique_ptr智能指针，这样子我们之后就不用再手动地释放指针对应的地址了。

General Matrix Multiply operation函数

Compute (`matrixA` * `matrixB` + `matrixC`).   * Return `nullptr` if dimensions mismatch for input matrices.

static std::unique_ptr<RowMatrix<T>> GEMM(const RowMatrix<T> *matrixA, const RowMatrix<T> *matrixB,
                                            const RowMatrix<T> *matrixC) {
    // TODO(P0): Add implementation
    auto matrixAmultB = Multiply(matrixA, matrixB);
    if (matrixAmultB != nullptr) {
      return Add(matrixAmultB, matrixC);
    }

    return std::unique_ptr<RowMatrix<T>>(nullptr);
  }

其他函数

T GetElement(int i, int j) const override {
    if (i < 0 || i >= this->rows_ || j < 0 || j >= this->cols_)
      throw Exception(ExceptionType::OUT_OF_RANGE, "index is out of range");

    return data_[i][j];
  }
void SetElement(int i, int j, T val) override {
    if (i < 0 || i >= this->rows_ || j < 0 || j >= this->cols_)
      throw Exception(ExceptionType::OUT_OF_RANGE, "index is out of range");

    data_[i][j] = val;
  }

结果

总结

project0还是偏简单的，根据一个矩阵的乘法来考察我们CPP的基本知识

世界并不是非黑即白的。